# 回溯算法used应该定义全局还是局部?
# 全局used
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
- 输入: [1,2,2]
- 输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]
该算法是一个常见的回溯问题,需要遍历所有的子树,同时进行集合去重
用示例中的[1, 2, 2] 来举例,如图所示: (注意去重需要先对集合排序)
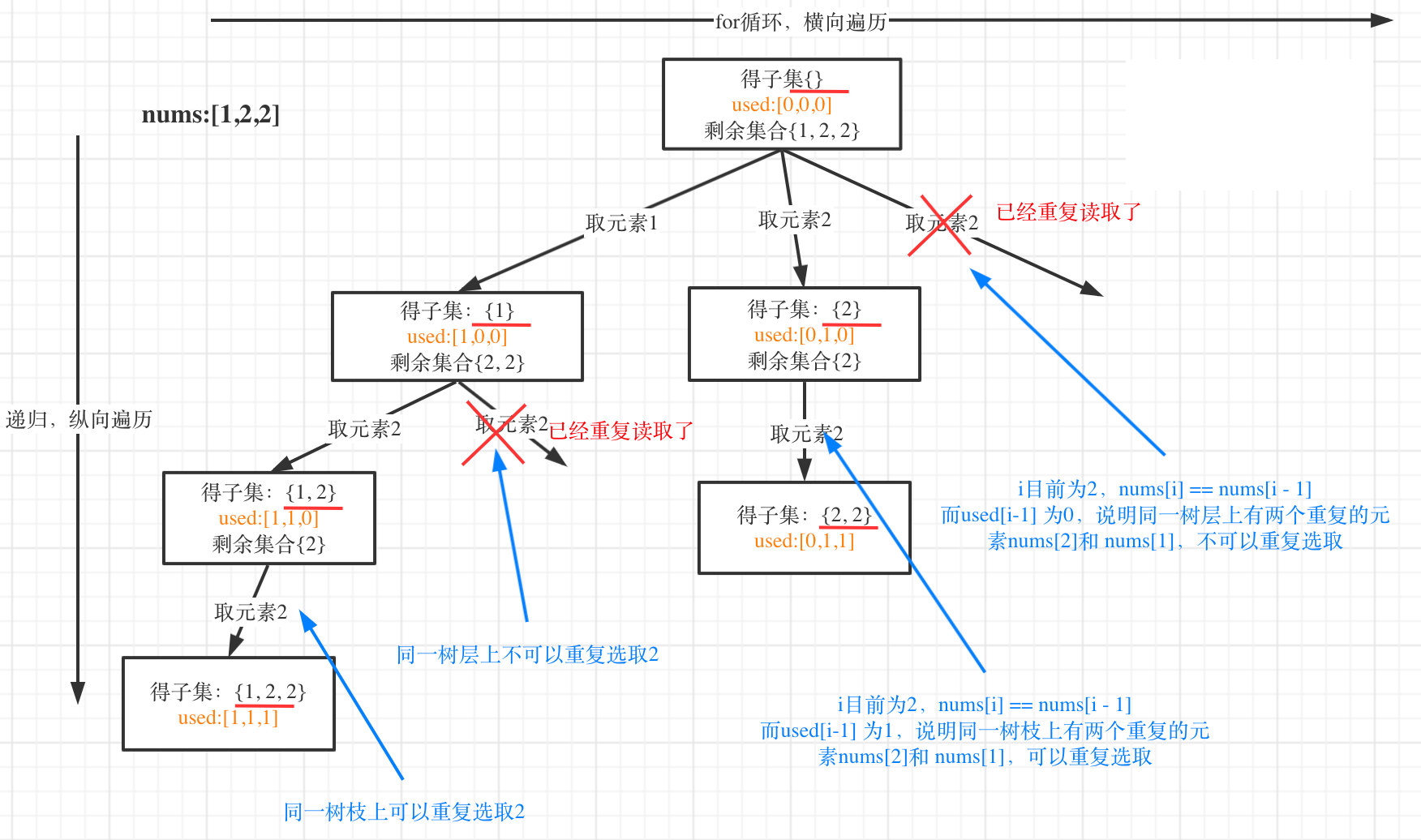
很容易得出c++代码如下:
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backtracking(vector<int> nums, int startIndex, vector<bool> used) {
if (startIndex > nums.size()) {
return;
}
res.push_back(path);
for (int i = startIndex; i < nums.size(); i++) {
if (i > 0 && nums[i] == nums[i-1] && used[i-1] == false) {
continue;
}
path.push_back(nums[i]);
used[i] = true;
backtracking(nums, i + 1, used);
used[i] = false;
path.pop_back();
}
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
if (nums.size() == 0) {
return res;
}
// 这里的used数组定义为全局变量
vector<bool> used(nums.size(), false);
sort(nums.begin(), nums.end());
backtracking(nums, 0, used);
return res;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# 局部used
给定一个整型数组, 你的任务是找到所有该数组的递增子序列,递增子序列的长度至少是2。
示例:
- 输入: [4, 6, 7, 7]
- 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
- 给定数组的长度不会超过15。
- 数组中的整数范围是 [-100,100]。
- 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况
和上题一样进行画图理解:
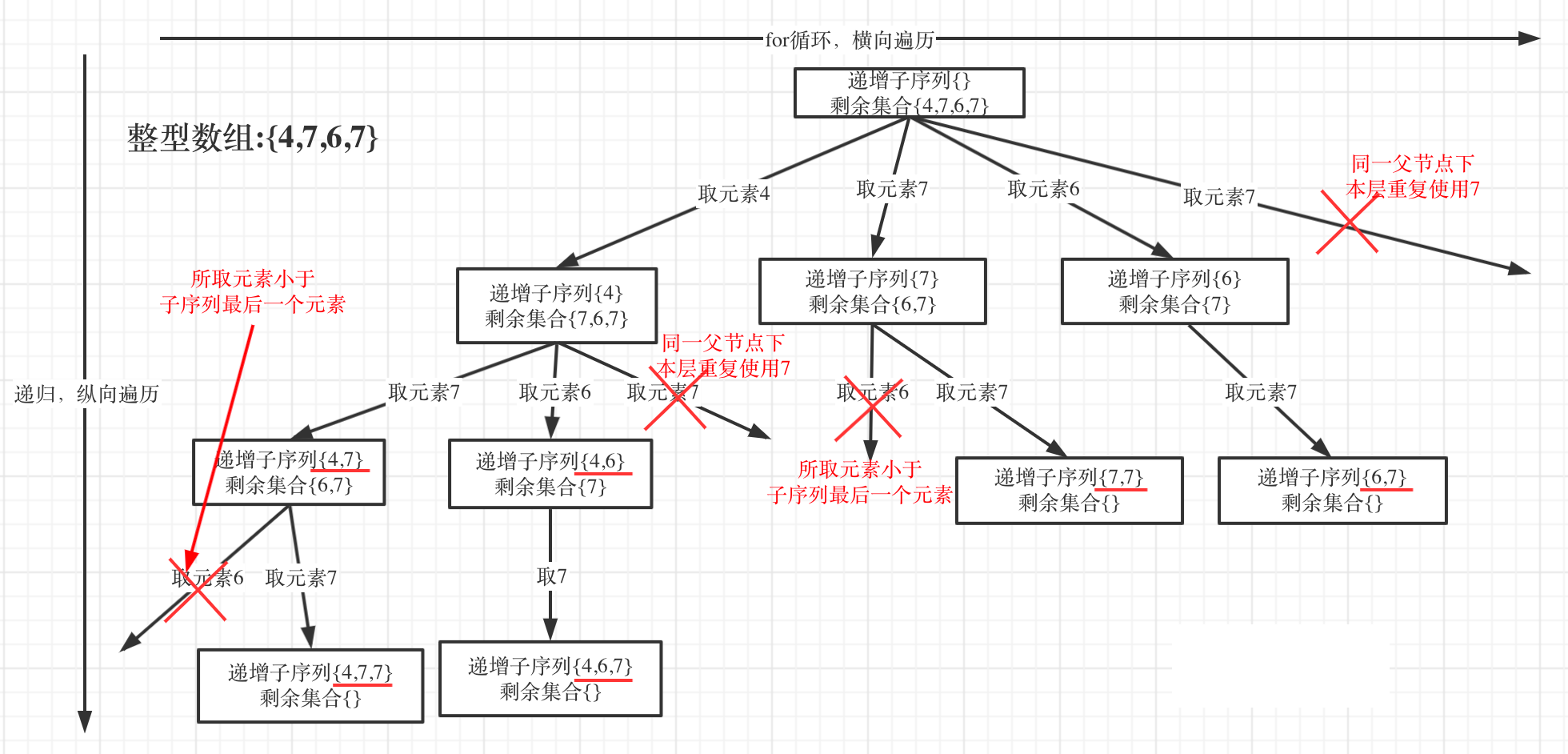
很容易得出c++代码如下:
class Solution {
public:
vector<vector<int>> res;
vector<int> path;
void backtracking(vector<int> nums, int startIndex) {
if (path.size() > 1) {
res.push_back(path);
}
// 这里定义为局部变量
int hash[201] = {0};
for(int i = startIndex; i < nums.size(); i++) {
if ((path.size() > 0 && nums[i] < path.back()) || hash[nums[i] + 100] == 1) {
continue;
}
hash[nums[i] + 100] = 1;
path.push_back(nums[i]);
backtracking(nums, i + 1);
path.pop_back();
}
}
vector<vector<int>> findSubsequences(vector<int>& nums) {
if (nums.size() == 0) {
return res;
}
backtracking(nums, 0);
return res;
}
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 如何选择?
通过上面的两种图可以注意到!
- 全局变量是对整个树的比较
- 局部变量是对树枝的比较
- 当回溯算法不需要关系其他分支的情况的时候选择局部used数组
- 通常情况下,需要考虑其他树枝的情况选择全局used数组

